Les suites de Queneau :

une histoire modèle et une morale élémentaire

 

 

Avant-Propos

C'est Jean Paulhan qui me présenta à Raymond Queneau, en 1946, je crois. Peu après, Boris Vian me donna l'occasion de le rencontrer à nouveau, dans un cadre plus familier. Ce fut le départ d'une amitié riche en discussions sur les sujets les plus divers : systèmes de la classification des sciences ^[1] , roller-catch, petits opéras, etc... En 1961, sur sa proposition et celle, conjointe, de François Le Lionnais, je fus élu membre de l'OULIPO.

A de nombreuses reprises Queneau avait attiré notre attention sur l'utilisation de contraintes numériques - voire de manifestations d'arithmomanie - en littérature. Mais ce n'est qu'en 1966 qu'il me parla des suites s-additives. J'avais alors la responsabilité de la Division de mathématique Appliquée à l'ESTEC (European Space technology Center), à Noordwijk (Pays-Bas) : cela me permit de traiter sur ordinateur un grand nombre de calculs qui, effectués "à la main", comme Queneau l'avait fait jusqu'alors, auraient pris un temps considérable et auraient sans doute être entachés d'erreurs.

Les suites s-additives (on dit aujourd'hui les "Suites de Queneau") ont été évoquées à plusieurs reprises, en particulier par François Le Lionnais ^[2] et Jacques Roubaud ^[3] . J'ai moi-même apporté ma contribution dans le Bulletin de la société mathématique de France ^[4] et dans le Magazine Littéraire ^[5] .

Mais je suis heureux d'avoir l'occasion, dans le cadre du colloque Qu'est-ce que le nombre?, de présenter quelques résultats nouveaux relatifs aux suites et d'en tirer quelques sujets de méditation. Une première version de ce travail a été présentée au Département de Mathématique de l'Université de Bordeaux I, le 9 février, puis a fait l'objet d'un séminaire du Centre de Poétique comparée, le 26 mars 1993.

 

1. Une histoire modèle

L'intérêt de Raymond Queneau pour les Mathématiques est ancien et multiforme. Il se manifeste de façon particulièrement claire dans Bords (Hermann 1963), recueil d'articles publiés entre 1935 et 1963, et où il est question des séries de Fourier, de Bourbaki... et des "conjectures fausses en théorie des nombres" ^[6] .

L'arithmétique exerçait un attrait particulier pour l'écrivain, attrait que manifestent aussi quelques articles de Bâtons, chiffres et lettres (Gallimard 1950, 1965) ^[7] et qui - de son propre aveu - allait jusqu'à l'arithmomanie : on connait le rôle des contraintes numériques dans la composition des romans et l'arrangement des poèmes (Morale Elémentaire comprend trois parties qui comportent respectivement 51, 16 et 64 textes; 16 et 64 traduisent des contraintes binaires hérités du Yi-King et de la tradition chinoise, le total - 131 - étant le plus petit nombre premier palindromique non trivial).

L'arithmétique est présente aussi dans Odile (Gallimard 1937) dont le narrateur est un mathématicien "raté" qui se perd dans des calculs et des élucubrations confuses. Il avoue :

... Je jetai un regard inopérant sur une feuille de papier qui traîne sur ma table : étant donnés deux rameaux réguliers simples à embranchements alternés, trouver le nombre de leurs points d'intersection en fonction des douze quantités dont dépend leur représentation symbolique par rapport à deux axes de coordonnées : qu'il fallut six quantités pour représenter sans ambiguïté une telle figure géométrique, c'était là, prétendais-je une de mes découvertes : en fait une simple constatation dont jusqu'à présent je ne savais rien déduire. Je pris un cahier ; il y avait là des calculs sur une nouvelle classe de nombres dont je me croyais le père, nombres formés de deux éléments extrêmes d'une double inéquation : ils présentaient par rapport aux trois opérations autres que l'addition des propriétés extrêmement curieuses que je n'arrivais pas à élucider entièrement ; des recherches sur ce que j'appelais l'induction des séries infinies et l'intégrale de Parseval, sur ce que je définissais comme l'addition à droite et l'addition à gauche des nombres complexes et l'importance de ces opérations pour l'analysis situs combinatoire. Chiffres, chiffres, chiffres...

On sait que Roland Travy, le narrateur, est très proche de Queneau, l'écrivain. Mais les recherches d'amateur un peu maniaque qui sont celles de Travy évoquent en réalité des recherches "sérieuses" - quoique marginales - de Queneau. Il n'aurait peut-être pas songé à les publier sans l'encouragement de mathématiciens "professionnels" et en particulier de Stanislaw Ulam et Gian-Carlo Rota, membres comme lui-même (ainsi que Claude Berge, Jacques Roubaud et l'auteur de cet essai) de l'OuMathPo créé par François Le Lionnais à l'image de l'Ouvrir de Littérature Potentielle, l'OuLiPo. L'OuMathPo fut d'ailleurs le premier des Ou-X-Po chers à l'auteur du Dictionnaire de Mathématiques, animateur infatigable de La Science en marche, etc...

2. Les suites s-additives

Queneau a publié deux textes sous le même titre : Sur les suites s-additives.

- Le premier est une note présentée à l'Académie des Sciences par André Lichnerowicz au cours de la séance du 6 mai 1968 (!). La note a été publiée dans le tome 226 A (p.957) des Comptes-Rendus;

- le deuxième est un article du Journal of Combinatorial Theory (12, p. 31, 1972) présenté par Gian-Carlo Rota.

La définition (telle qu'elle figure dans le second article) est la suivante :

Nous appelerons suite s-additive une suite S de nombres entiers positifs >0 strictement croissants:

u₁ ,u₂ ,..., u_n  ...

telle que:

   (a)   les 2s premiers termes sont donnés et forment la base de cette suite;

   (b)   pour n > 2s, u_n est le plus petit nombre entier plus grand que u_n-1 et tel que l'équation

ait exactement s solutions.

Pour qu'il y ait un terme et que la suite continue au delà de u_2s+1 , il faut que la base appartienne à l'un des s + 1 types explicités par Queneau, si bien que

Toute suite est donc donnée par les trois nombres s, u, v

On voit que si u et v ont un facteur commun, tous les nombres de la suite sont des multiples de ce facteur. On ne considérera donc que des suites telles que u = 1, v = 1 ou (u,v) = 1.

En faisant varier les paramètres - et en construisant, de proche en proche, les suites, on constate alors qu'elles manifestent les comportements les plus divers :

            - certaines sont finies (le nombre des termes et la valeur du terme final variant de               façon irrégulière avec les paramêtres)

            - certaines sont infinies mais se réduisent à des progressions arithmétiques "augmentées", ou à des combinaisons de telles progressions

            - certaines semblent erratiques (avec, dans certains cas, un segment initial "régulier", segment dont la longueur croît avec le paramètre v).

Les publications de Queneau formulent des conjectures et proposent des démonstrations. Les conjectures sont évidemment nourries par la construction explicite de suites. Il n'est donc pas inutile de diposer d'un algorithme de calcul effectif.

 

3. Construction et exploitation d'un algorithme d'engendrement des suites

Après la parution de la note aux Comptes-Rendus, j'avais entrepris de réaliser un programme informatique permettant d'obtenir automatiquement les suites lorsqu'on fournissait au système la valeur des trois paramètres. Le système de notation - devenu langage de programmation - inventé par Kenneth Iverson sous le nom d'APL ("A Programming Language) permettait de présenter une définition concise des suites ainsi qu'un algorithme de calcul. La définition se présente comme suit :

On appelle BQ la base de la suite, SQ le segment initial de la suite (jusqu'au terme d'indice n compris), NQ l'élément d'indice n +1, que l'on doit calculer à partir d'une suite déjà construite jusqu'à l'indice n.

Initialisation de la récurrence :

Le segment initial de SQ est une suite de 2s nombres > 0 strictement croissant

SQ  <— BQ

Explicitation de la récurrence :

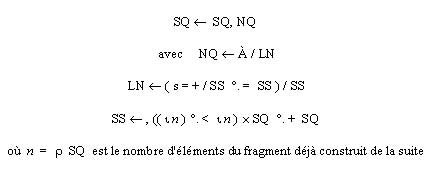
Dans la notation APL, /  représente le minimum et   . + donne la table d'addition de ses arguments. SS est donc le vecteur des sommes d'éléments de SQ pris deux à deux, (en éliminant ceux qui sont sur la diagonale ou au-dessus). Par ailleurs +/ SS . = SS donne le vecteur des nombres d'éléments identiques dans SS. LN est donc le vecteur des éléments de SQ qui ont exactement s couples d'éléments ayant la même somme.

Bien entendu cette formulation, qui a le mérite d'être purement algébrique, engendre des calculs (et des encombrements mémoire) en O (n²) et ne peut être utilisée que pour les petites valeurs de n. Des algorithmes plus traditionnels ont été programmés par la suite : en FORTRAN par Jacques de Meulenaar et Willy Lebrun, et, plus récemment en PASCAL par Eric Joncquel. Ce dernier  programme permet de visualiser les suites correspondant à une valeur donnée des paramètres, et jusqu'à un certain rang : dans la version actuelle on limite le nombre des termes à 2000 et la valeur du terme ultime à 30000. On a aussi la possibilité de construire des tableaux où, pour une valeur donnée de u, apparaissent, en fonction de s et de v, et lorsque les suitres sont finies, la valeur maximum atteinte par NQ, ou que l'indice n correspondant.

Des exemples de ces résultats sont proposés dans le paragraphe suivant. Dans tout ce qui suit, on se place dans le cas (le plus intéressant) où u = 1

Voici d'abord quelques exemples de suites finies (avec la valeur des paramètres correspondants)

s = 4, v = 5

1 12 36

2 14 38

3 16 47

4 18 48

5 20 49

6 23 51

7 25 53

8 27 60

9 29 80

10 31 85

s = 6, v = 7

1 11 28

2 12 31

3 13 33

4 14 35

5 16 37

6 18 39

7 20 41

8 22 43

9 24 50

10 26 63

s = 7, v = 12

1 15 26

2 16 28

3 17 30

4 18 32

5 19 38

6 20 40

7 21

12 22

13 23

14 24

s = 8, v = 10

1 12 24 47

2 13 26 49

3 14 28 51

4 15 31

5 16 33

6 17 35

7 18 37

8 19 41

10 20 42

11 22 44

Voici maintenant le segment initial d'une suite non bornée (c'est la suite d'Ulam) :

s = 1, v = 2 

1 26 72 131 197 258 356

2 28 77 138 206 260 358

3 36 82 145 209 273 363

4 38 87 148 219 282 370

6 47 97 155 221 309 382

8 48 99 175 236 316 390

11 53 102 177 238 319 400

13 57 106 180 241 324 402

16 62 114 182 243 339 409

18 69 126 189 253 341 412

Les tableaux suivants donnent, en fonction de v et s, la valeur du plus grand terme atteint.

a) 1 < s < 26, 2 < v < 26

b) 1 < s < 25, 25 < v < 51

c) 25 < s < 51, 25 < v < 51

4. Conjectures et problématique

Les résultats présentés dans le paragraphe précédent permettent d'évaluer les calculs effectués par Queneau et d'élaborer certaines conjectures. On est amené naturellement à se poser les questions suivantes :

Dans quelle condition les suites sont-elles finies

Pour les suites finies, existe-t-il une loi donnant le nombre d'éléments de la suite le dernier élément de la suite ou, dans un cas ou dans l'autre, une loi asymptotique? Pour les suites infinies, existe-t-il une formule donnant le terme d'indice n, ou le comportement asymptotique pour le terme d'indice n ? Plus généralement que peut-on dire de l'erraticité des suites?

On sait que l'intérêt d'Ulam pour la suite u = 1, s = 1, v = 2 était lié à la similitude du comportement de cette suite avec la suite des nombres premiers (y compris l'existence de termes "jumeaux").

Dans le cas des suites finies, et pour u = 1, pour s > 4 et v > 2s (avec cependant quelques exceptions pour v voisin de 2s ), les suites sont finies et se développent même de façon très semblable : pour une valeur donnée de s, le terme final augment de 4 lorsque v croît d'une unité (mais cet accroissement est de 10 pour s = 5 et de 8 pour s = 7. La croissance demeure irrégulière pour s = 9; d'ailleurs la suite s = 9, v = 43 semble infinie alors que toutes ses voisines sont finies.

Dans son article du Journal of Combinatorial Theory, Queneau définit des suites privilégiées, les suites naturelles, pour lesquelles v = (s + 1 ) u. Il donne aussi quelques théorèmes relatifs aux valeurs élevées de u, par exemple :

Pour u 3 et s > 1, toute suite s-additive est identique à la progression v + nu, avec un terme suppléméntaire u_i = 2v + (2s - 1)u, d'indice i = 3s + k + 1 (k étant donné par ku < v < (k + 1)u).

Il entame une étude détaillée des suites (s, 1, v) pour v > s + 1 et, dans le cas des suites naturelles (s, 2, 1), énonce des conjectures telles que :

Pour s 2 (mod. 3) les suites sont infinies.

Pour s 0 et s 1 (mod. 3) et s > 3, les suites sont finies.

Dans le dernier paragraphe de son article, Queneau propose quelques généralisations intéressantes et en particulier le concept de suite s'-additive : c'est une suite S' d'entiers strictement croissants telle que

(1) une base de 2s' entiers positifs est donnée;

(2) pour n 2s' + 1, u_n est le plus grand entier compris entre u_n + 1 et u_n-1 + u_n-2 et tel que l'équation :

u_n = u_i + u_j  (u_i u_j , i j,  u_i ,u_j S')

ait exactement s' solutions.

Les suites s'-additives naturelles sont celles dont la base est formée des s' premiers nombres entiers. Comme l'écrit Queneau :

Pour s' = 1, on a le plaisir de retrouver les nombres de Fibonacci.

Les suites s-additives et leurs variantes ne sont certes pas des objets mathématiques exceptionnels mais leur étude semble intéressantes pour des raisons essentiellement méthodologiques :

Leur définition ne fait appel qu'à deux concepts arithmétiques élémentaires : l'addition et l'inégalité. La formulation APL proposée dans le paragraphe 3 est entièrement algébrique.

Considérées comme définissant une fonction de l'indice, elles appartiennent à la classe des fonctions récursives non-primitives (en raison de l'existence du minimum dans la définition).

Leurs propriétés essentielles (finitude versus infinitude, régularité versus erraticité) manifestent une sensibilité remarquable à la variation des paramètres, sensibilité qui ne semble qu'imparfaitement maîtrisée par des assertions démontrables.

Cela semble être une situation idéale pour la mise en oeuvre de techniques propres à la théorie de la démonstration et à la théorie de la complexité : un terrain privilégié pour des travaux pratiques dans un domaine qui doit trop souvent demeurer dans l'abstraction.

De ce point de vue la rencontre avec Ulam est particulièrement significative : Ulam s'est intéressé à la suite {s = 1, u = 1, v = 2} dans le cadre de recherches intitulées On some mathematical problems connected with patterns or growth of figures ^[8] , recherches dont la première trace remonte à 1961 et qui sont liées aux modèles d'automates cellulaires auxquels s'intéressait aussi John Von Neumann. Les problèmes qui sont posés ici sont des problèmes profonds puisqu'ils ont trait aux propriétés de configurations finies dans leur développement combinatoire : ce sont des problèmes d'explicitation et d'évaluation de la complexité d'objets mathématiques susceptibles d'une définition élémentaire.

Ces problèmes ont une histoire relativement ancienne, mais curieusement discontinue :

- Le premier effort de spécification de la complexité d'un système formel (plus précisément de la "base d'un système normal") est dû à Emil Post et date de 1921. Il apparait dans un travail intitulé Absolutely unsolvable problems and relatively undecidable propositions : Account of an anticipation et fut proposé pour publication en 1941 ^[9] . On notera que Post s'efforçait d'élaborer une "psychological analysis of the mental processes involved in combinatory mathematics".

-  On rencontre ensuite Adolphe Lindenbaum et son exposé au Congrès international de Philosophie scientifique (Paris 1935), intitulé Sur la simpicité formelle des notions ^[10] (mais l'auteur souligne qu'il s'intéresse à ces notions depuis dix ans déjà).

-  Une notion voisine apparait dans un court article de Kurt Gödel Sur la longueur des   démonstrations ^[11] , publié en 1936.

-  A partir de 1943  (et jusqu'en 1955) paraissent des essais de Nelson Goodman (On the Simplicity of Ideas, The Logical Simplicity of Predicates, etc...). Ces articles entrainent des réactions de Kemeny, Suppes, Svenonius et les idées en sont reprises dans le livre  célèbre de Goodman The Structure of Appearance ^[12] mais demeurent apparemment sans lendemain.

- En 1964 Kolmogorov introduit le concept de la complexité d'un "objet fini" dans le cadre de l'étude des  systèmes formels algorithmiques. C'est le point de départ de recherches illustrées par Solomonoff, Martin-Löf, Chaitin, etc... où l'on étudie la complexité des calculs en liaison avec la théorie des fonctions récursives mais aussi en établissant des ponts avec des concepts comme ceux d'information et d'entropie ^[13] .

- En 1971 parait un rapport des laboratoires de Los Alamos intitulé The notion of Complexity, signé par W.A.Beyer, M.L.Stein et S.M.Ulam qui reprend l'étude de la complexité de structures algébrique simples, en particulier d'expressions arithmétiques et même tout simplement des nombres entiers ^[14] .

On arrive ainsi à cerner davantage des idées qui demeuraient un peu vagues comme celle de "richesse" d'un nombre, de "régularité" d'une suite numérique, etc... Les suites de Queneau sont alors des occasions précieuses de mettre à l'épreuve les tentatives de mesure de la complexité qui pourront être proposées.

5. Une morale élémentaire

Dans son article de la n.r.f. sur Queneau, François Le Lionnais rappelle que celui-ci était membre d'honneur de la "Confrérie des Dégustateurs de Nombre" qu'il avait créée - et qui ne se réunit jamais - initiative qui déboucha cependant sur la publication des Nombres remarquables. A vrai dire les nombres sont, chez Queneau un chemin pour voyager de la Science à la Littérature - et retour! Ils sont les témoins attentifs de cette durables célébration des Noces de la Science et de la Littérature qui fondent l'activité de ma Direction de Recherche au sein du Collège International de Philosophie.

En un parcours périphérique, il croit acquérir le numéro gagnant. Droits et pointés, gobins ou bien portant la double bosse, saturniens ou ventrus, monocyclistes, barrés, bicerclés, neufs ou oeufs, ils présagent un devenir meilleur. Harcelé, le flâneur confond nombres et chiffres. Il ne regarde que les rimes du trottoir, les cachets de l'asphalte (dates mémorables que nul ne collectionne), les ruisseaux peut-être méthodiques, les expectorations ou excrétions diverses. S'il levait le nez, il verrait au-delà des nuages les vérités arithmétiques, mais ce n'est que la nuit qu'il sombre dans le vertige des étoiles. Quand la roue a tourné, les miettes ne suffiraient même pas au rapiéçage d'une loque. c'est pourquoi, sans mélancolie notable, il prend la bûche pour la joindre au tas dont il faudra se chauffer pendant un hiver qui durera plusieurs saisons. Il finira par comprendre la loi de réciprocité quadratique en ses multiples démonstrations.