Le jardin des entiers qui bifurquent

 

Avant-Propos

Cet ouvrage rassemble des documents : textes de conférences ou rapports techniques, rédigés entre 1967 et 1993, mais repris et complétés ici pour que s'y manifeste une cohérence que je crois significative.

L'introduction s'appuie sur l'actualité, où l'on assiste à une prolifération d'idées originales relatives au concept mathématique et logique de nombre, en particulier de "nombre entier".Elle offre une vue d'ensemble de la problématique en s'efforçant de justifier la présence et d'évaluer l'importance des thèmes qui sont abordés successivement dans le texte : complexité, cercles "vertueux", dichômes.

           J'y reprends l'essentiel d'une séance de mon séminaire du Collège International de Philosophie (5 juin 1991) sur Les projets de formalisation universelle, séance intitulée : Trois binaristes témoins de leur temps : Brouwer, Chwistek, Ceccato. de la fatalité séquentielle. En avril 1986 j'avais déjà rassemblé les documents et l'argumentation de cet exposé sous la forme d'un "rapport ALAMO" intitulé Brouwer, Chwistek, Ceccato et l'univers des dichômes. Un examen plus particulier des systèmes de Chwistek avait été présenté au colloque "Mathematical Foudations of Computer Science" (Varsovie, août 1972), sous le titre Léon Chwistek and Computer Science. Plus récemment (mai 1992), j'ai eu l'occasion de faire le point sur l'analyse Ceccatienne, dans le cadre du séminaire de linguistique computationnelle de l'Université de paris XIII, avec une conférence intitulée Le serpent de mer des primitives sémantiques : un retour à Ceccato.

C'est une étude sur le problème mathématique de la complexité  qui constitue la deuxième partie du recueil. J'avais présenté  une communication à ce sujet au troisième Congrès "Logic, Methodology and Philosophy of Science" (Amsterdam, 25 août-2 septembre 1967) sous le titre "Le problème de Lindenbaum". Je repris ce travail en 1972, et cela fit l'objet d'une série d'exposés au séminaire ECSTASM (Expérience de Construction d'un Système de Traitement Automatique du Symbolisme Mathématique) qui se déroulait dans la cadre du Laboratoire "Al-Khowarizmi", au département de Mathématique de l'Université de Paris-Sud (Orsay), entre 1971 et 1975. Un résumé de ces exposés fut publié dans le bulletin C.D.I. "Informatique et Mathématiques Appliquées", édité par le centre de diffusion de l'innovation de l'ANVAR (N° 5, juillet-août-septembre 1972).

L'idée de la possibilité - et de la fécondité - du "renversement épistémologique" que l'on peut opérer en appliquant aux phénomènes de "limitation" de la Métamathématique l'argument même qui est à la base de ces limitations m'est venue au début des années soixante, en discutant avec Evert Beth du paradoxe de Berry et de l'interprétation "positive" qu'il en donnait (en définissant ce que j'appelle "la fonction de Berry-Beth"). Plus tard je découvris les possibilités de "circularité vertueuse" offertes par l'exploitation d'arguments ad hominem, chez Lorenzen, puis chez Fitch et d'autres. J'exposai les orientations nouvelles que ces observations me suggéraient à l'occasion d'un colloque intitulé "Modèles : formalisation et représentation", colloque organisé par le Groupe de Recherches Musicales de l'ORTF, en février 1977. La troisième partie de ce recueil est une mise à jour de mes réflexions à ce sujet.

Parmi les perspectives - méthodologiques et même épistémologiques - que peut ouvrir l'explicitation de schémas circulaires - mais créatifs - du processus cognitif, il en est une qui peut se révéler importante en Logique et en Linguistique et qui concerne des problèmes "sémantiques" comme ceux qui tournent autour des concepts de validité et de signification..

           C'est ainsi que, dans le cadre du laboratoire "Al-Khowarizmi", j'avais développé un algorithme de "typification" des termes du -calcul permettant d'automatiser les transductions qui assurent la "correspondance de Curry-Meredith". L'exploitation de cet algorithme suggérait une généralisation du concept d'expression algébrique (pour les -termes comme pour les "implications positives"), ce qui conduisit à un rapprochement que je crois fructueux entre les phénomènes de clôture et de véridiction. La quatrième partie de ce recueil donne un exposé succint de ces recherches, qui furent présentées au séminaire de Claude Berge (IHESSH) en 1982, puis au séminaire de Jacques Roubaud (Centre de Poétique Comparée) en 1983.

Dès les années quarante, c'est-à-dire au moment même de l'essor triomphal du Bourbakisme, j'avais été frappé par le caractère "figé" de la présentation axiomatique formelle des structures mathématiques. Avec Jacques Riguet, Marcel-Paul Schützenberger et, plus tard, Benoît Mandelbrot, je ressentais la nécessité d'une approche plus "dynamique". Ma rencontre avec le constructivisme, et, en même temps mon activité d'informaticien - et l'encouragement de Luitzen Brouwer, que je rencontrai à Blaricum en 1961 - me conduisirent peu à peu à imaginer une approche nouvelle qui rejoint, me semble-t-il, la réflexion de Benabou, Cartier, Lusson, Roubaud et d'autres, mais qui se développe aussi en parallèle avec une percée significative des nouvelles technologies (celles liées au traitement "hypermedia" de l'information). Cette approche fait l'objet de la cinquième - et dernière - partie de ce recueil, où je reprends et précise des arguments présentés en janvier 1977 à l'Atelier Scientifique de l'INA, sous le titre Formaliseme, déformalisme, transformalisme, arguments exposés sous un autre angle dans une communication au colloque des "Arts Electroniques", à Rennes, en juin 1989, sous le titre "Le dessein des mots animés". J'ai constaté d'ailleurs qu'une inspiration voisine se manifestait dans le livre récent de Pierre Lévy L'idéographie dynamique ^[1] .

La floraison proliférante que j'évoquais plus haut n'est pas fortuite : c'est l'aboutissement de recherches techniques précises qui réveillent des problématiques anciennes. De même les suggestions que j'apporte ne sont pas gratuites. Je suis au contraire convaincu que des applications spécialisées de la Mathématique, de la Métamathématique et de la Physique mathématique pouraient connaître des développements nouveaux - élimination de certaines divergences ou de certaines apories, efficacité accrue des procédures anticombinatoires - par la mise en ouvre des outils conceptuels qui apparaissent ainsi.

Bien entendu, une incitation non négligeable à rédiger tout ceci m'a été fournie par La Quinzaine littéraire ^[2] qui, en transcrivant le titre de la célèbre nouvelle de Borges avec une faute typographique, m'a gracieusement fourni le titre de ce travail.

 

 

Première partie

Un jardin extraordinaire

 

Chapitre 1

Une problématique "fin de siècle"

 

Le mois de juin 1993 aura été riche en actualité arithmétique : dix jours après le colloque "Qu'est-ce que le nombre", organisé conjointement par le Collège International de Philosophie et la Cité des Sciences et des Techniques de La Villette, sur l'initiative de Paul Henry et Jacques Roubaud, Andrew Wiles annonçait, pendant le séminaire "Fonctions-L et arithmétique" qui se tenait à l'Institut Isaac Newton, à Cambridge, une démonstration de la conjecture de Tamiyama-Weil (qui implique le "dernier" théorème de Fermat).

Un certain "retour à Fermat" est d'ailleurs dans l'air depuis un certain temps. On sait que la méthode dite de la "descente infinie" utilisée par le magistrat toulousain pour des démons-trations de théorèmes "négatifs" (par exemple "x⁴ + y⁴ = z²  n'a pas de solution non triviale en nombres entiers") indique la voie pour une arithmétique "constructive", c'est-à-dire, en particulier, n'utilisant pas l'axiome d'induction complète :

x [ y (y < x Ay) Ax] x Ax

lui-même déductible de l'axiome d'induction dans le système de Peano, axiome qui s'écrit

x [A0 x (Ax ASx)] x Ax

où S est la fonction "du suivant" (Sx = x + 1). Cet axiome "du premier ordre" exprime en réalité une infinité d'axiomes puisque la propriété A reste indéterminée. Une version "finie est celle du "second ordre " (on quantifie sur la "propriété" X) :

X [X0 y (Xy XSy)] y Xy

Yvon Gauthier (qui participait d'ailleurs au Colloque de La Villette) fait de la méthode de descente infinie le moteur essentiel de sa Logique interne, qui est une arithmétique tout autant qu'une logique. L'importance de cette problématique de l'induction transfinie - ou au contraire "effinie" comme le suggère Gauthier - vient évidemment de ce qu'elle se situe au cour du processus même d'engendrement des entiers.

Contrairement aux disciplines mathématiques "modernes" qui étudient les propriétés d'ensembles abstraits munis de structures spécifiques (algébrique, topologique, etc...), l'arithmétique ne décrit pas un ensemble, mais une suite. Contrairement aussi aux éléments d'un ensemble "usuel", les entiers ne sont pas des pions, figures anonymes d'un jeu réglé par un certain nombre de contraintes explicites, mais plutôt les témoins - les acteurs - d'une véritable histoire, emblèmes ou fétiches célébrés ou redoutés.

Dans les structures mathématiques "à la Bourbaki", on rencontre souvent des éléments distingués : élément neutre, idempotent, point d'accumulation, singularité, point fixe, etc... mais il s'agit toujours là d'objets singuliers. En arithmétique tous les nombres sont, d'une façon ou d'une autre,  singuliers ou remarquables ^[3] .

Il n'est donc pas étonnant que les suites numériques jouent un rôle essentiel en arithmétique. On peut citer :

De telles suites - on pourrait en citer d'autres - éveillent des désirs d'anatomie comparée, en raison de la simplicité de leurs définitions : les suites de Fibonacci ne mettent en jeu que l'addition, pour les nombres premiers c'est la multiplication. Pour les progressions il faut l'addition et la multiplication, pour Queneau l'addition et le minimum. Les énoncés "diophantiens" - y compris celui de Fermat - font aussi appel à l'exponentiation.  Il est alors tentant de construire des échelles de fonctions arithmétiques à partir de la fonction du suivant et de l'opérateur d'itération : on obtient ainsi successivement l'addition, la multiplication, l'exponentiation, la "tétration", etc... ^[5] La classification des fonctions récursives primitives proposée par Grzegorczyk systématise cette observation.

           Mais les exemples présentés plus haut montrent que le "rang", dans la hiérarchie de Grzegorczyk, des opérations nécessaires à la définition d'une suite n'en caractérise pas entièrement la "complexité" : l'articulation des concepts de base joue aussi un rôle qu'il n'est pas toujours facile d'identifier. J'y reviendrai dans la deuxième partie de ce travail.

Dans tous les cas, les suites "naturelles" d'entiers "naturels" se manifestent comme une sorte de déploiement. C'est l'aspect temporel de leur ontologie qui se manifeste ainsi et qui a été souligné par plusieurs mathématiciens et logiciens. C'est ainsi qu'entre 1909 et 1927, Moritz Pasch, célèbre par son axiomatisation de la géométrie projective, a exposé un programme fondationnel construit autour des notions de collectivité et d'événement, et où le concept arithmétique de succession se déduit du phénomène temporel de succession ^[6] . On sait que l'approche intuitionniste, plus connue, s'appuie essentiellement sur les concepts de suite de choix ^[7] , de déploiement, et exploite des arguments historiques ^[8] . La cinquième partie de ce travail y puise en partie son inspiration. Ainsi une problématique qui s'était précisée au début du siècle puis s'était estompée, retrouve, en cette fin de siècle, une prometteuse actualité.

 

Chapitre 2

Chantiers de l'innocence et de l'expérience

 

L'apparition des concepts de nombre entier et d'espace géométrique dans l'évolution culturelle de l'humanité ou dans l'évolution individuelle d'un être humain a fait l'objet de travaux nombreux - et parfois divergents - d'ethnologues, de linguistes et de psychologues. L'apparititon du nombre, en particulier, a été longuement étudiée et commentée ^[9] . Il est clair qu'une arithmétique véritable ne peut exister que dans un environnement culturel qui connait l'écriture.

Succédant aux images auxquelles on attribuait un pouvoir magique, les mots, auxquels "l'arbitraire du signe" donnait une étrangeté supplémentaire, gardèrent longtemps un parfum de surnaturel. Des hiéroglyphes aux écritures alphabétiques, la pratique du langage se précisait en une technique où les mots, les lettres, les nombres entiers jouaient leur partition en un contrepoint complexe. Dès la plus haute antiquité, le jeu des homophonies, puis l'utilisation de lettres pour représenter les nombres ouvrirent la voie à une arithmosophie aux aspects les plus divers.

Chez les Assyriens, les homophonies sont souvent exploitées pour transcrire les noms propres, proposant parfois aux savants des énigmes difficiles. C'est ainsi que le propriétaire de la tablette dite de l'Exaltation d'Ishtar (époque Séleucide) est désigné par l'inscription :

qu'on ne sait pas déchiffrer. La transcription numérique des noms propres, appliquée au nom des dieux peut donner lieu à des classements hiérarchiques ou même à des calculs : Gibil et Nusuku sont tous deux figurés par 10 car ils sont les compagnons de Shamash (2x10 = 20).

Le pouvoir gnoséologique des nombres entiers devient considérable avec le Pythagorisme et les diverses formes d'ésotérisme. Une version élémentaire de ces formes primitives du savoir est celle des chronogrammes que l'on trouve dans toutes les cultures où les entiers sont représentés par des lettres et non des signes distincts. Dans la Gnose et surtout dans la Kabbale, la mise en correspondance des alphabets (hébreu et arabe) et des nombres entiers permet d'associer à l'expression des événements un simple calcul.  En voici un exemple, dû à Al-Biruni (souvent appelé "Al-Khowarizmi"), où l'on déduit la date de l'Hégire (dans le calendrier Séleucide) de l'énoncé même de l'événement, en partant d'une correspondance précise entre lettres de l'alphabet arabe et nombres entiers :

Une arithmétique est ainsi à l'ouvre, porteuse d'une sémantique imaginaire aussi bien que d'une cryptographie "sacrée". D'ailleurs le mot sephiroth, ingrédient essentiel de la kabbale juive signifie "numérations". Plus généralement, guématrie est le mot utilisé par les juifs pour désigner le "calcul alphabétique" ou "évaluation numérique d'un mot". Les grecs utilisent pour cela le mot isopséphie et les musulmans l'expression Hisab al Jumãl.

C'est ainsi qu'en hébreu l'adage "in vino veritas" est justifié par l'équation "Yayin = Sod" (c'est-à-dire "vin = secret") que fournit l'évaluation numérique des letres :

Déjà Suétone, évoquant le meurtre d'Agrippine, en apporte la "preuve" arithmétique ^[10] :

Lorsque les nombres entiers acquièrent leur "indépendance symbolique" avec l'adoption de la numération de position et des "chiffres arabes", les tentations mystiques et magiques diminuent d'intensité sans toutefois disparaître totalement comme en fait foi la survie d'une tradition "ésotérique" illustrée par René Guénon (Raymond Queneau lui-même n'y fut pas insensible). Tandis que les savants découvrent de nouveaux sujets de perplexité avec les négatifs, les complexes, les irrationnels, les transfinis, etc... (adoptant souvent, dans une première phase, des qualificatifs péjoratifs : nombres "négatifs", "imaginaires", "impossibles", etc...), un large public reste sensible à la magie des nombres : rôle privilégié (positif ou négatif) des entiers 2, 3, 7, 12, 13, 32, 666, etc... Bâtons, chiffres et lettres (le titre d'un ouvrage de Raymond Queneau!) participent ainsi à un concert où les mélomanes sont des "arithmomanes".

Une problématique marginale mais assez fascinante en surgit parfois. Je citerai le problème (bien connu des bibliothécaires) du classement alphabétique des noms de nombres (en français et dans plusieurs autres langues, la suite des entiers, pour illimitée qu'elle soit, n'enpossède pas moins un dernier terme qui est évidemment zéro!). Plus excitant sans doute est le problème de Perec : trouver les couples de nombres premiers dont la représentation décimale est en miroir et où le plus grand est égal au double du plus petit moins un. Le couple { 37, 73 } répond évidemment à la question; mais en existe-t-il d'autres? ^[11]

 

Chapitre 3

Mariages et divorces de l'arithmétique et de la logique

 

On assiste, depuis le début du siècle, à un débat de "priorité" relatif à la logique et à l'arithmétique. A la suite de Frege, puis de Russell, Carnap, etc... l'avantage a été donné à la logique qui, à condition d'être correctement formalisée, devait assurer le fondement de l'activité mathématique et permettre ainsi une validation de toute construction théorique. Mais à plusieurs reprises des voix discordantes se sont élevées, venant surtout des rangs "constructivistes", qui mettent au contraire au premier rang l'activité mathématique, et plus précisément l'activité arithmétique considérée comme première à toute autre.

Dès 1907, au début du Chapitre III de ce qui sera la version imprimée de sa thèse, chapitre intitulé Mathematics and Logic, Brouwer place un paragraphe au titre significatif : Mathematics is independant of logic. Il défend sa position dans sa correspondance avec son directeur de thèse, D.J. Korteweg, en ces termes :

Tout récemment Yvon Gauthier propose à son tour une "logique interne" de nature essentiel-lement arithmétique. Il précise :

Si l'on se trourne vers l'histoire pour éclairer le débat, on observe que

dans l'antiquité les deux activités demeurent distinctes, la logique étant un objet privilégié d'affirmation et de polémique pour de grandes écoles de pensée comme celles des péripatéticiens, des stoïques, des sceptiques, de Mégare, etc... D'ailleurs Eubulide et Chrisippe sont bien antérieurs à Euclide, Eratosthène et, bien entendu, Diophante ^[14] . La situation est semblable dans l'évolution des savoirs orientaux, de la Chine et de l'Inde, comme pour la rhétorique des romains.

la transmission, par l'Islam, du savoir héllénistique s'accompagne d'une fission entre la logique et l'arithmétique. De Scot Erigène à Abelard, des grandes écoles de pensée médiévale jusqu'à Port-Royal, de la logique arabe au syllogisme rabbinique, c'est la logique qui est le lieu privilégié des controverses et des progrès de la pensée abstraite en s'efforçant d'expliciter son articulation avec le langage avec la question des universaux, l'étude de la suppositio, des particules syncatégorématiques, bref, la théorie du raisonnement. L'arithmétique est surtout un calcul et sert de modèle à une algèbre en cours de constitution. Une logique formelle constituée dans le cadre d'une méthodologie proprement mathématique n'apparaît qu'avec Leibniz à la fin du XVII^ème siècle.

le retard historique de la logique apparaît clairement lorsqu'on regarde de près les techniques de la formalisation. L'apparition des symboles est tardive pour l'arithmétique:

- les signes + et - n'apparaissent qu'en 1481, = en 1557, en 1631

- les techniques d'arrangement syntaxique des expressions et des formules ne se précisent qu'à la fin du quinzième siècle (utilisation du point . ou de l'arceau pour lier les symboles, exploitation des parenthèses, des crochets et du vinculum,  superposé chez Cavalieri (1647), sous-posé chez Bombieri (1550) ^[15] ,

mais elle est encore plus tardive pour la logique. Il faut attendre G. Boole et l'Analyse mathématique de la Logique (1847) pour qu'un système de symboles - d'ailleurs emprunté à l'arithmétique - soit mis en ouvre. Les symboles proprement logiques ne sont adoptés qu'à la fin du XIX^ème siècle et, aujourd'hui encore, ne font pas l'objet d'un total consensus. En 1872, Grassmann utilise encore le vinculum superposé pour exprimer la négation (le signe n'apparaît qu'en 1912, dans les Principia). Peano - le grand créateur de symboles - garde le "-" pour la négation, mais propose et pour les connecteurs logique "et" et "ou" (les Principia utilisent le "." multiplicatif pour "et", mais le signe nouveau pour "ou") ^[16] . Dans son Begriffschrift (1872) Frege introduit un système de notation multilinéaire dont subsiste seulement le symbole d'assertion .

L'objectif poursuivi par les animateurs de l'Ecole de Turin : Peano, puis Padoa et Burali-Forti était double : intégrer la réflexion logique dans la technique mathématique et constituer une idéographie (ils utilisent aussi le mot pasigraphie) spécifique :

              Tout en se conformant à la méthode de Boole, M. Peano se trouva ainsi amené, par les exigences même des applications qu'il se proposait d'en faire, à y introduire des modifications et des additions, contenant les germes des perfectionnements ultérieurs qui lui permirent [...] d'écrire ses Arithmetices principia en se passant complètement du langage ordinaire.

              On comprend aisément que dans une même proposition, il ne pouvait pas donner aux mêmes signes un rôle arithmétique et un rôle logique; c'est pourquoi il représenta les concepts logiques par des signes spéciaux ^[17] .

Avec la diffusion du Formulaire de Mathématique de Peano ^[18] , et des Principia Mathematica de Whitehead et Russell ^[19] , les années vingt sont celles des logiques polonaises. Les innovations notationnelles se multiplient : technique de "préfixage" de Lukasiewicz, symbolismes déviants de Lesniewski et de Chwistek, etc...

L'arithmétique n'a pas totalement disparu puiqu'on dénote souvent par 1 et 0 les "valeurs de vérité" vrai et faux (les "tables de vérité" n'étant ainsi que des tables de Pythagore à quatre éléments). Mais elle revient en force avec le codage numérique (par des nombres premiers) des symboles de la logique, codage utilisé pour la première fois par Gödel dans sa démonstration :

"0" –› 1, "f" –› 3, " ~ " –› 5, " √ " –› 7, " Π" –› 9, "(" –› 11, ")" –› 13 ^[20] .

 

Chapitre 4

Quelques logiques buissonnières

 

Ainsi les acquis - souvent amers - de l'expérience conduisent les mathématiciens à retrouver les chemins de l'innocence, où ils espèrent assurer enfin la sécurité de leur démarche. C'est évidemment la motivation essentielle du "Programme de Hilbert" : on n'est vraiment à l'aise que dans la manipulation de nombres entiers finis et, si possible, petits. Dans son traité de Logique déductive, Padoa glorifie l'exploit de Peano qui "réduit le vocabulaire logique à une ligne", ligne composée de seize caractères, mais qu'il réussit à limiter finalement à trois : " =, et " ^[21] . Plus tard, soucieux de mettre de l'ordre dans les extension successives de la notion de nombre, il s'efforce à nouveau de réduire le nombre des "idées primitives" : deux pour la théorie des nombres "entiers absolus", trois pour la théorie algébrique des nombres entiers positifs ou négatifs, etc... ^[22] Se laissant emporter par l'enthousiasme, Padoa déclare :

- En conclusion, l'ère des extensions successives de l'ensemble des nombres est close et le plus vaste ensemble de nombres, digne de ce nom, est celui des nombres complexes ordinaires...

Le succès d'entreprises de ce genre (les polonais y apportent une contribution importante) est lié à la disponibilité d'un outillage formel efficace et sûr. En particulier la restriction à un petit nombre de primitives impose la mise en ouvre, à tout instant et en tout lieu du raisonnement, des mécanismes délicats de la définition et de la substitution. Or le traitement des malaises engendrés, au début du siècle par la mise à jour des antinomies de la théorie des ensembles amène un renouvellement considérable de la problématique en précisant les conditions de bon fonctionnement de ces mécanismes :

les problèmes de la substitution reçoivent un traitement complet dans le cadre de la Logique combinatoire de Curry et du -calcul de Church. Ces systèmes, dont le "pouvoir" est équivalent à celui des systèmes de Post, Gödel, Kleene, Turing, Markov, n'en présentent pas moins - tout comme eux - des "limitations" calculatoires symbolisées par le "combinateur paradoxal" de Curry.

l'examen des conditions de catégoricité d'une définition, dans un système formel spécifique, met au jour, par le biais du théorème de Löwenheim-Skolem, la possibilité de définir et d'utiliser des êtres mathématiques, notamment des nombres, non-standards.

On reprendra, dans la deuxième partie de ce travail, l'examen des techniques de réduction définitionnelles : elles débouchent naturellement sur la problématique de la complexité. Cette problématique a été renouvelée récemment dans le cadre d'une confrontation avec les domaines de la calculabilité, de l'information et même, par ce biais, de la Thermodynamique ^[23] . Mais au centre de l'argumentation on rencontre toujours les apories de la circularité dont le "renversement" fera l'objet de la troisième partie. Diverses voies s'offrent alors à ceux qui cherchent à franchir ou à contourner les obstacles qui se dressent ainsi. Dans la quatrième partie je présenterai une "étude de cas" fondée sur une sorte de "complétion" de la correspondance de Curry, ouvrant ainsi des perspectives de "dynamisation" à la Pasch.

Mais auparavant je voudrais tirer la leçon de la multiplication récente de propositions  relatives à l'élargissement du concept de nombre. Car ces propositions mettent en jeu, sous une forme ou sous une autre, un même famille d'objets mathématiques : celle des arbres.

Les premières extensions du concept de nombre étaient essentiellement des complétions : symétrisation d'une loi de composition interne associative et commutative, complétion topologique, etc... Les nouvelles mettent plutôt en jeu des techniques combinatoires, un thème largement négligé par la vulgate bourbakiste. Ces techniques sont utilisées à des fins de représentation : représentation des objets et représentation des structures.

Ici ce sont les linguistes qui ont montré la voie. En 1939, Lucien Tesnière avait déjà mis au point une technique de représentation des structures syntaxiques par des arborescences d'un type spécial, auxquelles il avait donné le nom de stemma ^[24] . Mais les logiciens avaient pris les devants : inspiré par Husserl et Brentano, Kazimierz Ajdukiewicz ^[25] , puis Yehoshua Bar-Hillel définissaient des grammaires de catégories débouchant sur une représentation arborescente (implicite) des syntagmes, représentation adoptée ultérieurement par Chomsky.

Il fallut attendre 1958 pour cette technique soit utilisée pour expliciter la structure de ce type particulier de phrase qu'est une expression mathématique. Voici un exemple, proposé par le logicien polonais Roman Suszko ^[26] :

 

Les arbres d'Ajdukiewicz étaient implicites. Il en va de même d'arbres particuliers, dicho-tomiques, utilisées par des philosophes et des logiciens pour le codage des objets logiques ou linguistiques eux-mêmes - y compris les entiers.

Le pionnier est, ici encore, Brouwer qui déclare dans sa thèse (1907) :

Dans son dernier article important : Points and spaces ^[28] , il est encore plus clair :

Brouwer prétend fonder ainsi l'existence des entiers, des opérations arithmétiques, etc... Il ne propose cependant pas de formalisation et demeure circonspect relativement au système de logique intuitionniste développé ultérieurement par Heyting, puis par Kleene et d'autres.

Paradoxalement c'est un "méthodologue" soucieux des problèmes épistémologiques du "langage naturel" qui offrira une formalisation (graphique) d'un système dichotomique tout à gait demblable, système conçu d'ailleurs dans l'ignorance des textes de Brouwer - qui n'étaient alors disponibles qu'en néerlandais! Dans La machine qui pense et qui parle ^[29] , Silvio Ceccato s'exprime ainsi :

                    La chose qui dure deux temps est l'élément corrélateur, les choses qui se substituent sont les corrélats, premier et second.

Sur cette base, Ceccato tente une sorte de reconstitution phénoménologique formalisée du langage et de la pensée, offrant un modèle "vinculaire" pour de nombreux concepts, mots et même énoncés tels que le cogito ergo sum de Descartes et le verum factum convertuntur de Vico. C'est ainsi que - s désignant un "état de conscience", il propose les représentations suivantes :

s s s	s s s s	s s s s s	s s s s s	s s s s s s s s	s s s s s s s s s
sujet	singulier	pluriel	un	et	ou

Ceccato utilise aussi d'autres notations équivalentes à celle-ci, et dont l'une est une variante de la "notation polonaise" ^[30] .

Une notation du même type est à l'ouvre dans les systèmes logiques développés par Léon Chwistek et son école (à Cracovie et à Lwow) dans les années trente. Chwistek - qui proposa un peu avant Ramsey une version "simplifiée" de la théorie des types - se propose moins de représenter les concepts que d'en assurer une codification systématique. Il s'agit d'édifier un système formel complet de la "Science rationnelle", incluant la logique, la sémantique, etc... A la base un alphabet de deux signes, ♦ et c , ainsi qu'une règle de construction récursive des expressions :

- c est une expression

- si E et F sont des expressions, ♦ EF est une expression

Au moyen d'une série de codages de plus en plus complexes, Chwistek édifie une hiérarchie de systèmes formels : systèmes propres, métasystèmes, métasystèmes généralisés ^[31] . Contraire-ment à Brouwer et Ceccato, il commence par la codification des entiers qu'il conduit de la façon suivante :

les entiers "naturels" reçoivent des codes "symétriques"

♦ cc est le code pour 0

♦ ♦ cc ♦ cc est le code pour 1

...

♦ ♦ nn ♦ nn est le code pour n+1

des mots "asymétriques" sont introduits

♦ ♦ cc ♦ ♦ cc ♦ cc est le code pour I

♦ ♦ ♦ cc ♦ cc ♦ cc est le code pour II

on construit alors une logique formelle à partir du connecteur de Scheffer (non-et)

♦ ♦ I E ♦ II F est le code pour la proposition E/F

si E sont les codes de deux propositions

etc...

Bien que la tâche que Chwistek s'était fixée n'ait pas été complètement achevée, ce que nous connaissons de son travail donne à penser qu'une reconstruction cohérente et consistante d'un système formel de la mathématique serait possible sur cette base ^[32] .

Ce que je voudrais seulement souligner ici, c'est l'efficacité d'un codage dichotomique des entiers, codage qui, avec des variantes, va trouver une utilisation nouvelle dans un certain nombre de propositions récentes d'extension du concept de nombre entier ^[33]

Chapitre 5

Le champ du signe

 

Les objets mathématiques évoqués dans le chapitre précédent n'ont rien de mystérieux : ils sont simplement des symbolisations variées d'éléments "du magma libre à un générateur ou du système de tous les parenthésages possibles" comme l'observe Pierre Cartier qui adopte le codage suivant des entiers naturels (j'adopte ici la présentation "polonaise" préfixée, plus aisément manipulable typographiquement) :

♦	♦cc	♦c ♦cc	♦c ♦c ♦cc
0	1	2	3

 

Ces jeux de notation ne sont pas sans intérêt : ils illustrent le rôle des conventions grammaticales qui, dans le langage naturel comme dans les langages formels, permettent de vaincre cette "fatalité séquentielle" (l'expression est de Raymond Queneau) que nous imposent les contraintes de l'expression orale ou écrite. Dans le cas de formules algébriques, la linéarisation fonctionne par projection de l'arbre syntaxique sur les axes de coordonnée d'un système de référence arbitraire, comme le montre l'exemple du mot représentant le concept de point (punto) dans le système de Ceccato :

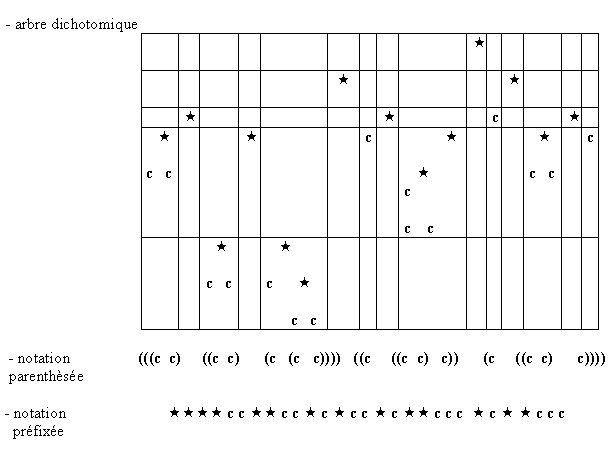
On voit que la notation parenthésée s'obtient par projection verticale, et la notation préfixée (resp. postfixée) par une projection horizontale vers la gauche (resp. droite) sur un axe oblique.

Mais la très grande simplicité de ce codage dichotomique ne doit pas dissimuler quelques problèmes techniques sur lesquels je voudrais attirer l'attention (leur importance apparaîtra dans les parties ultérieures de ce travail).

Ces problèmes s'inscrivent naturellement sous trois rubriques : explicitation des structures, ap-profondissement de la nomenclature, techniques de la représentation.

-             Le choix de la technique de représentation est affaire de commodité. On notera cependant que la notation mathématique traditionnelle n'est guère cohérente : on trouve simultanément des notations infixées ( a + b ), préfixées ( Max a,b ), postfixées ( a! ), et même circumfixées ( a ) ^[34] . La notation arborescente s'avère donc préférable lorsque les expressions atteignent une certaine longueur. Dans le cas du langage naturel une telle notation s'est d'ailleurs révélée fort utile, que ce soit pour des grammaires de dépendance comme celle de Tesnière ou pour des grammaires de constituants à la Chomsky.

              L'exemple de la linguistique me permet aussi d'évoquer le problème des relations (ana-phoriques, par exemple), qui obligent à sortir du domaine strictement arborescent. L'utilisation des schémas et diagrammes dans la théorie des catégories en est un autre exemple. Les formes modernes d'argumen-tation mettent de plus en plus souvent en valeur des schémas de contre-réaction comme ^[35]

-              Si les contraintes de l'écriture usuelle forcent la linéarité de l'expression, les contraintes du dessin sur l'espace à deux dimensions d'une feuille expriment implicitement un ordre partiel des objets attachés au sommet des "arbres". Or, dans la nomenclature standard ^[36] , une arborescence est un arbre muni d'une racine; un arbre est un graphe connexe sans cycles; un graphe est un couple composé d'un ensemble (et non d'une séquence) de sommets et d'un ensemble de flèches reliant deux de ceux-ci : dans une arborescence, les successeurs d'un sommet ne sont pas ordonnés ! Les objets utilisés par Chwistek, Tesnière , Ceccato,Cartier, Benabou, Roubaud et beaucoup d'autres ne sont donc pas des arborescences - et encore moins des arbres - sinon, pour Ceccato, "temps" serait identique à "espace", alors que

♦♦♦♦ccc♦ cc♦ cc    est visiblement différent de     ♦♦cc ♦♦♦ccc ♦cc

et pour Benabou la multiplication des entiers "surnaturels" serait commutative, alors que

{ ♦ccc } x{ ♦cc } = { ♦♦cc♦cc♦ cc } est différent de { ♦cc } { ♦ccc } = { ♦♦ccc♦ccc }

Il serait raisonnable d'utiliser pour ces objets une désignation spécifique : pourquoi pas stemma?

-              Le développement de systèmes de manipulation formelle assistée par ordinateur a conduit à rechercher d'autres modes de représentation car le déchiffrement d'une notation polonaise ou parenthésée passe par une analyse syntaxique tandis que la la représentation bidimensionnelle, malgré les progrès de la technique informatique, n'est pas d'une manipulation aisée. Aussi utilise-t-on souvent, dans le cas des 1-graphes quelconques,  la matrice d'incidence qu'illustre ci-dessous le 1-graphe donné en exemple par Berge, qui figure ici avec sa matrice associée :

	x1	x2	x3	x4	x5	x6
x1		1
x2	2	3	4	5
x3
x4			6
x5
x6					8	7

 Une version plus économique (en quantité de mémoire consommée) consisterait, lorsque le nombre maximal des successeurs d'un sommet est petit, à utiliser une matrice ayant un nombre de lignes égal au nombre des sommets, et un nombre de colonnes égal au nombre maximal de successeurs d'un sommets, plus un : la première colonne contenant la liste des sommets et, pour chaque ligne, l'identificateur d'un sommet étant suivi des identificateurs de ses successeurs. Dans le cas d'un stemma n'ayant que deux ou zéro successeurs, une matrice à trois colonnes fait l'affaire ^[37] . On aura ainsi, pour  l'analyse Ceccatienne du mot "temps", en plus de la version polonaise donnée plus haut :

 

(dans la dernière version, l'étiquetage illustre la non-pertinence d'un "ordre" des sommets).

Bien entendu les manipulations (humaines) seront facilitées par l'utilisation d'étiquettes plus traditionnelles telles que les identificateurs alpha-numériques. Les manipulations informatiques, pour leur part, mettent en jeu des pointeurs qui sont en fait des nombres entiers dénotant des adresses.

La suite de ce livre nous donnera l'occasion d'approfondir certains aspects de ces techniques de représentation. Mais on peut noter dès à présent que

-   L'introduction d'objets formels nouveaux pour représenter les nombres - en premier lieu les nombres entiers, mais aussi d'autres notions linguistiques et logiques - passe par une analyse de ces notions en constituants considérés comme plus élémentaires. D'atomes syntaxiques et sémantiques, ces objets sont transformés, par une sorte de "zoom" méthodologique, en structures combinatoires finies susceptibles d'entrer dans un jeu d'opérations spcécifiques : concaténation, insertion, coupure, etc...

-   La possibilité d'une telle analyse entraine un perméabilité nouvelle des frontières entre les domaines de l'arithmétique, de la logique et de la linguistique. Il se développe ainsi un "espace épistémo-logique" où des auteurs comme Chwistek, Ceccato, Wilks, Wierzbicka pourraient se retouver ^[38] .

On peut donc espérer que certains aspects des problèmes e la vérité et de la signification pourront ainsi être posés en des termes nouveaux, techniquement plus précis, donc susceptibles d'une évaluation rationnelle. A titre d'exemple j'évoquerai le problème (traditionnel) de l'adéquation du conenant au contenu. C'est un problème immense, dans le cas général, puisqu'il recouvre aussi bien les figures de la rhétorique, de l'allégorie à la synecdoque et à la métonymie, que les pratiques de la symbolisation : emblème, idéogramme, icône, signe abstrait; mais c'est un problème plus accessible, évidemment, quand on se limite au domaine de l'arithmétique.

Pour les petits nombres entiers, c'est une notation analogique qui s'impose souvent au départ. Les bâtons viennent avant les lettres et les chiffres, comme en témoignent les écritures suivantes :

 

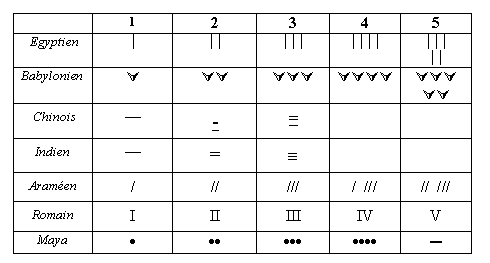
Ce tableau appelle les remarques suivantes :

- pour n = 1, 2, 3, tous les systèmes fonctionnent par concaténation itérée

- la direction de concaténation est en général horizontale mais peut devenir verticale

- à partir de 4, de nouveaux signes peuvent apparaître ou une nouvelle direction de

  concaténation s'ajouter à la première

Les nouveaux nombres (ces "entiers qui bifurquent") sont souvent associés à des arbres (ou plutôt des stemmas) dont les branches font songer aux encoches ("tallies") des notations primitives, dans la mesure où ils s'efforcent d'associer aux concepts premiers de l'arithmétique : opération du "suivant", addition, etc... des manipulations élémentaires comme la concaténation. On le voit sans peine lorsqu'on traduit en stemmas les notations de Chwistek, Cartier, Benabou, Lusson... et l'on retrouve ainsi avec plaisir des figures voisines de celles que nous proposent un système de notation numérique secrète turque ^[39] :

On voit ici à l'ouvre ce qu'on pourrait appeler une approche non-saussurienne, puisque refusant "l'arbitraire du signe". Une approche semblable (mais qui demeurera inexploîtée) se trouve aussi dans une proposition de Lesnewski pour la notation des connecteurs booléens.

Les connecteurs les plus utilisés sont évidemment et et ou, qui expriment d'ailleurs ce qu'on a appelé le "parallélisme logico-grammatical". Si l'on représente les "valeurs de vérité" par 1 et 0 (vrai et faux), chaque connecteur peut être associé à sa "table de Pythagore" qui est ici une matrice booléenne à deux lignes et deux colonnes : il y a donc seize tables possibles (dont plusieurs sont triviales). Lesnewski a eu l'idée d'associer à chacune de ces possibilités un symbole spécial dont le graphisme correspond directement au contenu de la matrice (ou "table de vérité") ^[40] . Voici la table contenant ces connecteurs (dans leur symbolisme usuel, lorsqu'il existe) associés à leur table de vérité et au symbole de Lesnewski correspondant :

Contrairement au domaine "booléen" où l'ensemble de base, réduit à deux éléments, est strictement fini, le domaine des entiers se trouve placé, quel que soit le système de notation utilisé - fut-il puissant comme le système hiérarchisé "Archimède-Ackermann" - devant le gouffre du dénombrable non-borné. Une correspondance - bien différente des précédentes - entre graphes (non orientés) et nombres entiers nous entraine même vers le non-calculable ^[41] . L'explosion combinatoire est donc encore plus redoutable que la simple fuite en avant. On verra, dans la deuxième partie, comment la recherche d'une mesure, ou tout au moins d'une expression de la complexité nous incite naturellement à la spécification de "nouveaux entiers".

Les mécanismes de l'itération et de la récursion évoquent aussi la structure d'un schéma en boucle. La troisième partie sera consacrée à l'examen des mécanismes paradoxaux qui trouvent leur expression naturelle dans de tels schémas. On montrera que ces schémas, à côté des limitations que l'on peut en déduire, possèdent aussi un versant productif dont on peut donner une représentation graphique - ou plutôt matricielle - éclairante. La quatrième partie mettra ces techniques en applications en étudiant une généralisation possible de la "correspondance de Curry". On introduira ainsi de nouveaux objets finis combinatoires qui se situent peut-être à la limite du domaine des "nouveaux entiers".

Depuis l'invention des automates cellulaires par John von Neumann et Stanislaw Ulam, on sait que les objets combinatoires sont chargés d'une dynamique potentielle des plus riches. Une telle dynamique peut à son tour donner lieu à une réalisation analogique : celle que permettent aujourdh'ui les nouveaux supports de l'information. La cinquième partie de cette étude examinera les conditions de mise en ouvre de ces nouvelles technologies et leurs conséquences pour une arithmétique - voire une mathématique - nouvelle.

On parlait autrefois du "jardin des racines grecques". De nouvelles pépinières sont ouvertes aujourd'hui où s'épanouissent les espèces inédites que notre imagination a dessinées jardins de papier ou de pixels où se joue le miracle d'un herbier qui refleurit.