Clef du site

Elle réside dans l'examen d'un paradoxe :

le paradoxe des unités opérationnelles
dans le calcul analogique

qu'illustre le schéma ci-dessous :

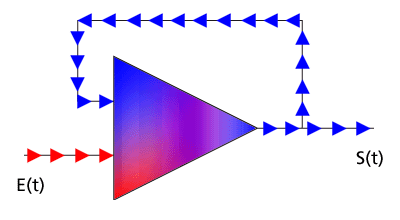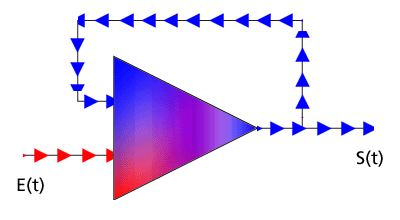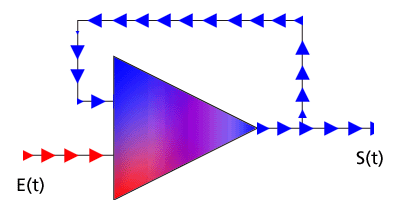
Ce schéma a été conçu de façon à fournir, à la sortie de l'unité opérationnelle, la valeur opposée à celle qui est imposée à l'entrée "externe" (il s'agit en général de tensions électriques) :

S(t) = - E(t),

ce qui équivaut à

S(t) + E(t) = 0.

Au sein du triangle fonctionnel (un amplificateur à courant continu - à très grand gain) la tension électrique à l’entrée, E(t), et la tension de sortie S(t) s’ajoutent algébriquement en raison du bouclage de la sortie sur l’entrée, ce qui donne, à l'entrée "interne" :

e(t) = E(t) + S(t).

A la sortie, on retrouve cette valeur multipliée par le gain G de l’amplificateur. Comme ce gain est très grand, e (t) doit être très petit pour que la sortie effective,

S(t) = G * e (t),

ait une valeur finie. S(t) est donc très voisin de – E(t), ce qui est le résultat désiré (mais seulement presque ce résultat). Et puisque e (t) est très précisément l’erreur commise dans ce calcul on arrive à ce paradoxe :

la solution n’existe que parce qu’elle est entachée d'une erreur

(et elle lui est même proportionnelle!)

Cette observation est, selon moi une clef de la recherche braffortienne.

Elle combine le thème de la boucle, qui est le fondement des théorèmes de limitation en logique, avec celui de l'amplification (sous la forme particulière d'une "avalanche sémantique" à la Themerson), des thèmes dont on trouvera l'utilisation dans plusieurs incursions de l'auteur dans les domaines de la linguistique, mais aussi de la physique théorique.

W.H.